Noha a GIS szoftverek többsége támogatja a 3D szerkesztési lehetőséget, azonban a poligon 3D területszámítás máig egy komoly problémát jelent. Ez a problémakör köszönt vissza, amikor a tetőelemző szkriptet írtuk mivel ehhez is szükséges a QGIS 3D területszámítás, azaz a poligonok felszínének kalkulációja.
Jelenlegi cikkünkben a poligon QGIS 3D területszámítás problémakörét, a megoldást jelentő szkriptet és a QGIS alatti megvalósítást mutatjuk be.
A poligon 3D területszámítást azért QGIS alatt mutatjuk be, mert az nyílt forráskódú, így bárki számára elérhető. Az általunk bemutatott metódus használható akár ArcGIS alatt is, azonban ott a geometriai adatok kinyerésére arcpy függvényt kell alkalmazni.
Megjegyzés: A QGIS 3D területszámítás kiváltható akár Blender Computer Graphics szoftverrel. Blenderben nem szükséges kódot írni, azonban a Blender GIS és a 3D-Print Toolbox addon-ok telepítésére szükség van, ha shapefile területét szeretnéd kiszámolni.
Alapvető probléma
A GIS szoftverek alapvetően térképi megjelenítésre és térkép alapú elemzésekre lettek kitalálva. A 3D világba való bekapcsolódás később érkezett ebbe a technológiába. A térképi vetülettel rendelkező geometriák területének kiszámítását magabiztosan és nagy pontossággal végzik.
Általános esetben a poligon 2D területszámítás a Heron képlettel végezhető el. A GIS szoftverek ezt kiegészítik a koordináta referencia rendszer (CRS) sajátosságaival. Nézzük meg, hogy milyen beépített QGIS területszámítások érhetők el!
- $area – Visszaadja az aktuális elem területét. Ennek a funkciónak a segítségével kiszámított terület figyelembe veszi az aktuális projekt ellipszoid beállításait és a terület mértékegység beállításait is. Például ha az aktuális projektben ellipszoid van beállítva, akkor a kiszámított terület ellipszoidális lesz, és ha nincs ellipszoid beállítva, akkor a kiszámított terület síkbeli lesz.
- area – Visszaadja a poligon objektum területét. A számítások mindig síkbeliek lesznek a geometria koordináta referencia rendszerében (CRS), és a visszaadott terület mértékegységei megegyeznek a CRS mértékegységeivel. Ez eltér az által a $area függvény által végzett számítástól, ami az aktuális projekt ellipszoidjára és terület mértékegység beállításaira alapozva ellipszoidális számításra képes.
Tehát bármelyik QGIS területszámítást használjuk is, mindkét esetben kettő dimenzióban számolva kapjuk meg a poligon területét hiába hoztunk létre 3D poligont (PolygonZ). A poligon QGIS 3D területszámítás eggyel bonyolultabb művelet és ez sajnos nem része a QGIS beépített függvényeinek.
Python 3D területszámítás Stokes képlettel
A QGIS 3D területszámítás megfelelő alkalmazásához számos fórumot, tudományos cikket és GitHub repository-t végignéztünk, mire rátaláltunk caougolin python kódjára. Ő a Stokes képletet használta fel, hogy egy általános python kódot írjon a poligon 3D területszámításra. Caougolin megoldásával QGIS 3D területszámítás python kódot írtunk. A továbbiakban bemutatjuk az eredeti python kódot, majd az általunk felhasznált verziót.
Caougolin a Stokes függvényt felhasználva a következő 3D poligon területszámítás kódot írta meg.
import math
def compute_3D_polygon_area(points):
if (len(points) < 3): return 0.0
P1X,P1Y,P1Z = points[0][0],points[0][1],points[0][2]
P2X,P2Y,P2Z = points[1][0],points[1][1],points[1][2]
P3X,P3Y,P3Z = points[2][0],points[2][1],points[2][2]
a = pow(((P2Y-P1Y)*(P3Z-P1Z)-(P3Y-P1Y)*(P2Z-P1Z)),2) + pow(((P3X-P1X)*(P2Z-P1Z)-(P2X-P1X)*(P3Z-P1Z)),2) + pow(((P2X-P1X)*(P3Y-P1Y)-(P3X-P1X)*(P2Y-P1Y)),2)
cosnx = ((P2Y-P1Y)*(P3Z-P1Z)-(P3Y-P1Y)*(P2Z-P1Z))/(pow(a,1/2))
cosny = ((P3X-P1X)*(P2Z-P1Z)-(P2X-P1X)*(P3Z-P1Z))/(pow(a,1/2))
cosnz = ((P2X-P1X)*(P3Y-P1Y)-(P3X-P1X)*(P2Y-P1Y))/(pow(a,1/2))
s = cosnz*((points[-1][0])*(P1Y)-(P1X)*(points[-1][1])) + cosnx*((points[-1][1])*(P1Z)-(P1Y)*(points[-1][2])) + cosny*((points[-1][2])*(P1X)-(P1Z)*(points[-1][0]))
for i in range(len(points)-1):
p1 = points[i]
p2 = points[i+1]
ss = cosnz*((p1[0])*(p2[1])-(p2[0])*(p1[1])) + cosnx*((p1[1])*(p2[2])-(p2[1])*(p1[2])) + cosny*((p1[2])*(p2[0])-(p2[2])*(p1[0]))
s += ss
s = abs(s/2.0)
return s
polygon = [[0,0,0],[0,1,0],[1,1,1],[1,0,1]]
result = compute_3D_polygon_area(polygon)
A 3D területszámítás a gyakorlatban
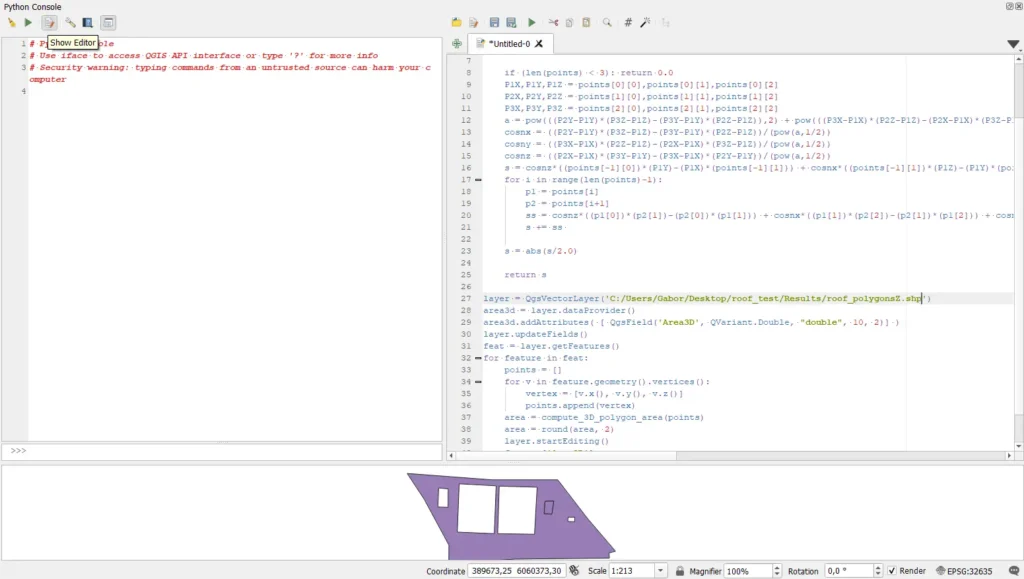
A QGIS 3D területszámítás gyakorlati oldalát mutatom be, tehát hogy hogyan is kell használni a Stokes képlet alapján készült python kódot. A QGIS-t elindítva nyisd meg a python konzolt (Ctrl+Alt+P).
Megjegyzés: Az általunk írt python kód alkalmas PolygonZ típusú geometria 3D területszámításra. Továbbá, a bonyolultabb, gyűrűkkel rendelkező poligonokkal is megbirkózik!
Kattints a “Show Editor” gombra. A jobb oldali részbe lehet python kódot írni.
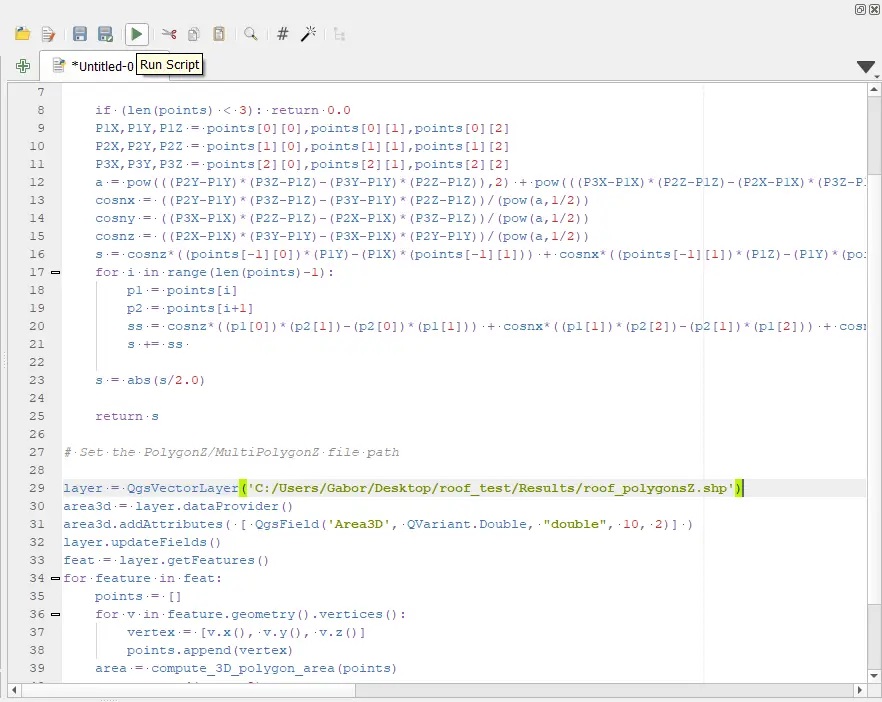
Másold ki és illeszd be a következő kódot. Ügyelj arra, hogy a “layer = QgsVectorLayer(‘PATH’)” résznél a PATH helyére beírd annak a poligonnak az elérési útját, aminek szeretnéd kiszámolni a 3D területét.
from qgis.core import *
from PyQt5.QtCore import *
import math
def compute_3D_polygon_area(points):
if (len(points) < 3): return 0.0
P1X,P1Y,P1Z = points[0][0],points[0][1],points[0][2]
P2X,P2Y,P2Z = points[1][0],points[1][1],points[1][2]
P3X,P3Y,P3Z = points[2][0],points[2][1],points[2][2]
a = pow(((P2Y-P1Y)*(P3Z-P1Z)-(P3Y-P1Y)*(P2Z-P1Z)),2) + pow(((P3X-P1X)*(P2Z-P1Z)-(P2X-P1X)*(P3Z-P1Z)),2) + pow(((P2X-P1X)*(P3Y-P1Y)-(P3X-P1X)*(P2Y-P1Y)),2)
cosnx = ((P2Y-P1Y)*(P3Z-P1Z)-(P3Y-P1Y)*(P2Z-P1Z))/(pow(a,1/2))
cosny = ((P3X-P1X)*(P2Z-P1Z)-(P2X-P1X)*(P3Z-P1Z))/(pow(a,1/2))
cosnz = ((P2X-P1X)*(P3Y-P1Y)-(P3X-P1X)*(P2Y-P1Y))/(pow(a,1/2))
s = cosnz*((points[-1][0])*(P1Y)-(P1X)*(points[-1][1])) + cosnx*((points[-1][1])*(P1Z)-(P1Y)*(points[-1][2])) + cosny*((points[-1][2])*(P1X)-(P1Z)*(points[-1][0]))
for i in range(len(points)-1):
p1 = points[i]
p2 = points[i+1]
ss = cosnz*((p1[0])*(p2[1])-(p2[0])*(p1[1])) + cosnx*((p1[1])*(p2[2])-(p2[1])*(p1[2])) + cosny*((p1[2])*(p2[0])-(p2[2])*(p1[0]))
s += ss
s = abs(s/2.0)
return s
# Set the PolygonZ/MultiPolygonZ file path
layer = QgsVectorLayer('PATH')
area3d = layer.dataProvider()
area3d.addAttributes( [ QgsField('Area3D', QVariant.Double, "double", 10, 2)] )
layer.updateFields()
feat = layer.getFeatures()
for feature in feat:
points = []
for v in feature.geometry().vertices():
vertex = [v.x(), v.y(), v.z()]
points.append(vertex)
area = compute_3D_polygon_area(points)
area = round(area, 2)
print(area)
layer.startEditing()
feature['Area3D'] = area
layer.updateFeature(feature)
layer.commitChanges()
QgsProject.instance().reloadAllLayers()
print("Done!")
A kódot a “Run script” zöld háromszög gombbal tudod lefuttatni.
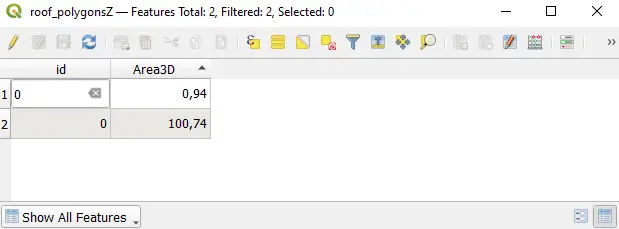
Az eredmény a poligon attribútum táblájában jelenik meg. Fontos megjegyezni, hogy csak akkor működik a 3D területszámítás, ha az attribútum táblázatban nincs még olyan nevű oszlop, hogy “Area3D”!
A QGIS 3D területszámítás limitációja
Fontos megjegyezni, hogy a QGIS 3D területszámításnak is megvan a limitációja. Csak olyan poligonnak lehet kiszámolni a 3D területét, amelynek a csúcsai sorrendben vannak rendezve. Más szóval a sorrendiség azt jelenti, hogy bármely ponttól kezdődhetnek a poligon töréspontjai, de vagy az óramutató járásával megegyező vagy azzal ellentétes irányba kell haladnia. Egy átlagos vektorizálás pontosan így halad, de jobb erre külön is felhívni a figyelmet. Ha a csúcsokat nem sorrendben adjuk meg, akkor a 3D területszámítás eredménye 0 lesz.
Továbbá, a QGIS 3D poligon területszámítás nem alkalmazható 2D poligonokon. A 2D poligonok esetében a 3D területszámítás eredménye “Not a Number” (NaN) lesz. Nem ad megfelelő eredményt olyan MultiPolygonZ geometria esetében, ami egynél több részből áll.
záró gondolatok
A QGIS-ben végzett műveletek során számos esetben hasznos lehet, ha ki tudjuk számolni egy adott poligon 3D területét. A SurveyTransfer is használ 3D területszámítást, ami hasonlóképp működik az itt leírt módszerhez.
A SurveyTransfer csapata a tetőelemző megoldásához fejlesztette a QGIS 3D területszámítás szkriptet.
Ha nagyon-nagyon tetszett, amit olvastál, akkor meg is oszthatod az ismerőseiddel. Ne fogd vissza magad! 🙂
Tetszett, amit olvastál? Akarsz hasonlókat olvasni?